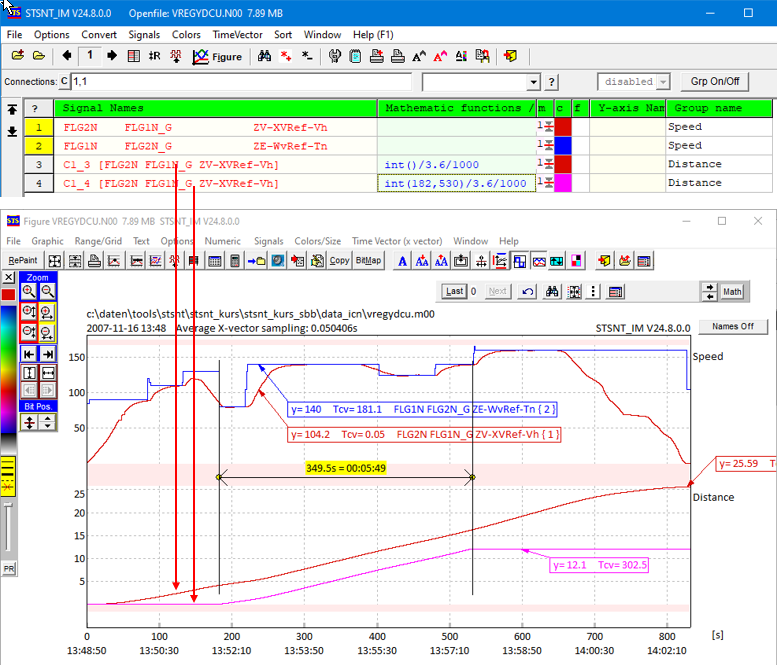
1. Integrating of signals
The example shows the speed of a train with demanded and actual speed (with speed control) up to 140Km/h.
The speed (signal 1) must be integrated to get the distance!
For this, to keep the original signal, a copy must be made for integrating the whole time range;
only as example for alimited integrating range, a second copy of the speed is made :
- For whole range, select integration function with empty brackets: int(), then divide by 3.6 (Km/h -> m/s) and divide by 1000 to have distance in Km (option)
- For limited time range: int(182,530), then dito like point 1
In the graphic you will see result:
- brown signal: at the end of the run the distance is 25.59Km
- pink signal: distance between the integration points is 12.1Km
The distance can now be used as new x vector to have the distance instead of time!
This will be explained in an other section.